Estimado Arquimedes:
Soy Euler del futuro, te escribo desde mi habitación en San Petersburgo (Rusia), para explicarte mi teorema de Poliedros a pesar que he sufrido unas graves fiebres y he quedado ciego, sigo trabajando gracias a la ayuda de mi hijo mayor, que ve por mi.
He estudiado tu teoría sobre poliedros, donde comentabas que un grupo de poliedros convexos tiene las caras como polígonos regulares de dos o mas tipos y que todos tus sólidos tienen los vértices uniformes y te comento mi teoría y mis conclusiones:
Mi teorema indica la relación entre el numero de caras, aristas y vértices d un poliedro convexo.
Teorema delos poliedros
C+V=A+2
DONDE:
C=Num de caras.
V=Num de vértices
A=Num de aristas
N Num de lados del polígono regular
R=Num de aristas que convergen en los vértices
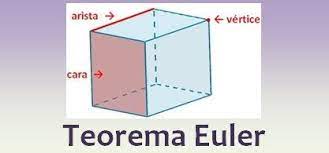
EJEMPLOS:Para un cubo se tiene que C=6 A=12 V=8, por lo que aplicamos la formula
C+V=A+2 y nos da 6+8=12+2
Los casos mas conocidos corresponden a los poliedros regulares: Tetraedro,cubo,octaedro,dodecaedro e icosaedro.
Un saludo
Euler