Estimado colega, soy Augustin Louis Cauchy matemático francés de la École Polytechnique de París.
Me dirijo a usted Bernard Bolzano para agradecerte sus contribuciones a las matemáticas y en particular a las funciones continuas. Gracias a ellas me dediqué y me inspiré para investigar sobre mi teorema, pero antes me voy a presentar. Como ya he dicho me llamo Augustin Louis Cauchy y nací el 21 de agosto de 1789 empecé a educarme con mi padre, y más adelante estudié en la escuela politécnica de París en la que destaqué siendo un buen estudiante en el que obtuve el título de ingeniería civil. Posteriormente, me dediqué a la investigación científica intensiva y a la publicación de varias obras importantes. Una de mis principales aportaciones se basa sobre la demostración del teorema del número poligonal de Fermat al que se habían dedicado varios matemáticos como Gauss. Fui nombrado profesor de mecánica en la École Polytechnique en 1816 además de ser nombrado miembro de la Academia Francesa de las Ciencias en lugar de Gaspar Monge, que como bien sabrá fue expulsado por razones políticas.
Como venía diciendo me he inspirado en su teorema, gracias a él me interesé por las funciones continuas y sus características, de ahí empecé a desarrollar mi teorema. Éste se fundamenta en lo siguiente:
Dadas dos funciones f(x) y g(x) continuas en un intervalo [a,b] y derivables (a,b) existe un punto c en el que las derivadas (la pendiente de una recta tangente en ese punto) de esas funciones guardan una relación proporcional.
[f(b) – f(a)]/[ g(b) – g(a)] = f’(c)/g’(c)
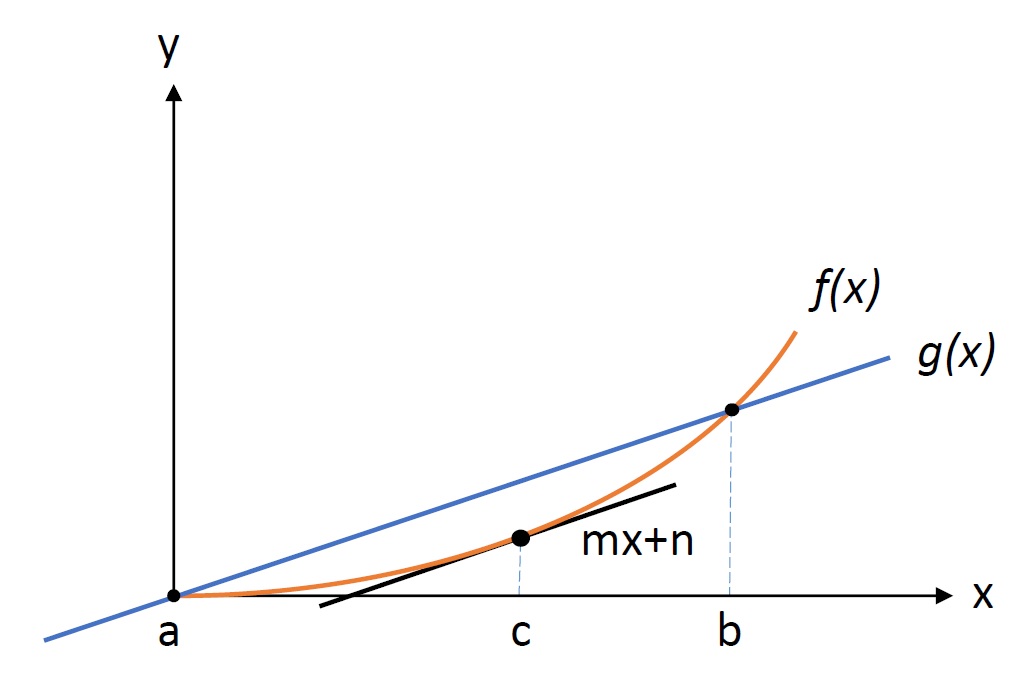
Para poder explicárselo mejor, permítame darle una visión geométrica de lo que esto significa. Tomemos como ejemplo una función curva sencilla f(x) y una recta secante a ésta como g(x). Si tenemos en cuenta estas condiciones, la ecuación anterior tiene un valor igual a uno. Esto implica que existirá en el intervalo [a,b] un punto c en el que la derivada de la curva f(x) en el c (f’(c)) tiene la misma que la secante tal y como se representa en la siguiente figura.
Ha sido un placer poder contarle mis avances sobre las funciones continuas, espero que siga teniendo grandes contribuciones en este campo y que podamos seguir cartearnos sobre estos temas.
Un cordial saludo
Augustin Louis Cauchy
Profesor de la École Polytechnique de París
25 de marzo de 1823