Estimado colega
Me llamo Agustín Louis Cauchy matemático francés de la École Polytechnique de París. Probablemente no me conocerás porque no soy de tu época, aun así, te escribo para darte las gracias por haber aportado a este mundo de las matemáticas en el que todos estamos inmersos un granito de arena. También me entristece no poder habernos conocido en persona pero las circunstancias no lo permiten. Principalmente me pongo en contacto contigo para poder comunicarte que tu teorema, el teorema de L’hopital se complementa con mi teorema, ahora tu teorema se puede llevar más a la práctica y se puede demostrar de forma mucho más formal gracias a mis aportaciones. También he entablado buenas relaciones con Bernarnd Bolzano, que además es un matemático magnifico, que también está interesado en las funciones continuas y todo lo relativo a la continuidad y derivabilidad de las mismas. Hemos desarrollado muchos proyectos juntos y hemos hecho grandes aportaciones al campo de las matemáticas.
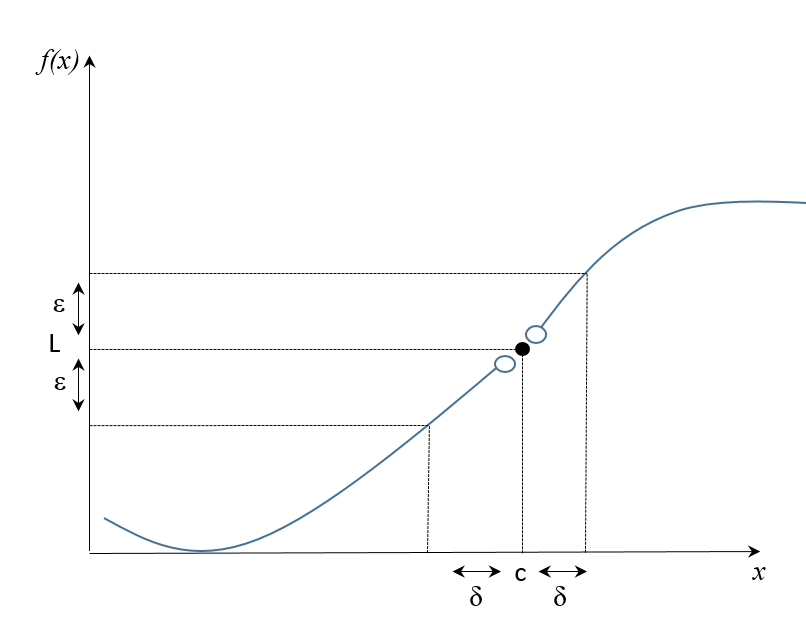
Enfocándonos más en ti, he comprendido tu teorema a la perfección y me parece de lo más interesante. Si tenemos en cuenta el cálculo de límites en las funciones, que es una herramienta fundamental para poder determinar el valor de las funciones cuando existen indeterminaciones. A continuación, te adjunto una gráfica de la definición de límite para poner en contexto tu teorema
Por lo que he analizado, se basa en calcular el límite de una relación de funciones según la siguiente formulación:
Por lo que he visto, este teorema es algo muy útil y que nos permitirá resolver problemas de límites cuando existan indeterminaciones de forma muy sencilla, será bastante útil en un futuro cercano. Te he tenido también de inspiración además de referente en toda mi obra científica. Ha sido un placer hablar contigo y poder haber contribuido a las matemáticas juntos
Un saludo
Agustín Louis Cauchy